SADER METHOD
AFM Cantilever Calibration

Overview

The spring constants of AFM cantilevers are often required in applications of the AFM. For force measurements where normal deflection of the cantilever is monitored, the normal spring constant, which relates the applied normal force to the normal deflection of the cantilever, is required (see Fig. 1 for a schematic).

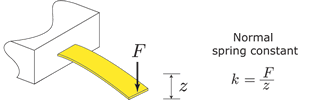
Fig. 1: Schematic illustration of the normal spring constant.

In Lateral Force Microscopy, the torsional spring constant, which relates the applied torque to the angle of twist of the cantilever is important (see Fig. 2 for a schematic).

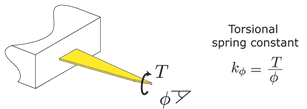
Fig. 2: Schematic illustration of the torsional spring constant.

Here, we briefly outline the Sader method for calibrating the normal spring constant of rectangular AFM cantilevers, as well as the Torsional Sader method which enables the calibration of the torsional spring constant of rectangular AFM cantilevers. We also describe the physics underpinning the method and its extension to cantilevers of arbitrary shape.

First, though, we note that both techniques require the plan view dimensions of the rectangular cantilever (length and width), which can be obtained with sufficient accuracy using an optical microscope. Furthermore, the resonant frequency and quality factor of the peaks are also needed. These are typically obtained by measuring the thermal noise spectra of the unloaded AFM cantilever, and fitting the response of a Simple Harmonic Oscillator (SHO) with added white noise floor,

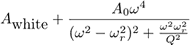
to the fundamental power spectrum resonant peak, see Fig. 3.

Fig. 3: SHO fit to thermal noise power spectrum. The red line is the response of a SHO, whilst the black circles are experimental data from the thermal noise spectrum.

Once the required quantities are measured, the normal and torsional spring constants of the cantilever can be determined using the Sader method [1], [4], provided that the following conditions are met:

1. That the length of the cantilever greatly exceeds its width, which in turn greatly exceeds its thickness;
   
   
2. That the quality factor is much greater than unity.

In practice, the first requirement is typically satisfied for practical rectangular cantilever, whilst the second requirement is usually satisfied when the cantilever is immersed in air.

Sader method

The normal spring constant of a rectangular AFM cantilever can be determined using the Sader method [1], which states

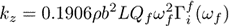
where L and b are the length and width of the cantilever, respectively, ρ is the density of the fluid, ω_f and Q_f are the (radial) resonant frequency and quality factor of the fundamental resonance peak, respectively, and Γ_i^f is the imaginary part of the hydrodynamic function given by Eq. (20) of Ref. [2].

In order to assist the user, the Sader method has been implemented in an online calibrator, meaning that no code needs to be written by AFM users.

Torsional Sader method

The Sader method was extended to allow calibration of the torsional spring constant of rectangular AFM cantilevers [4], using the result

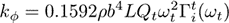
where L and b are the length and width of the cantilever, respectively, ρ is the density of the fluid, ω_t and Q_t are the (radial) resonant frequency and quality factor of the fundamental torsional resonance peak, respectively, and Γ_i^t is the imaginary part of the hydrodynamic function given by Eq. (20) of Ref. [5].

Again, in order to assist the user, the Torsional Sader method has been implemented in an online calibrator.

Cantilevers of arbitrary shape

The extension of the Sader method to cantilevers of arbitrary shape is reported in [6], [7]. This includes an explanation of the underlying physical basis of the method, its validity in the presence of nonidealities, such as added spheres or tips, and its general applicability to small elastic bodies of arbitrary shape and composition.

iPhone and web apps that implement the Sader method for rectangular and arbitrary cantilevers are available at the links at the top of this page.

Global Calibration Initiative (GCI)

The Sader Method GCI [7] - available via link at the top of this page and sadermethod.org - enables the standardisation of cantilever calibration, for cantilevers of any type and shape, utilising data from the worldwide AFM community.

References

1. J. E. Sader et al., Review of Scientific Instruments, 70, 3967 (1999).


2. J. E. Sader, Journal of Applied Physics, 84, 64 (1998).


3. J. W. M. Chon et al., Journal of Applied Physics, 87, 3978 (2000).


4. C. P. Green et al., Review of Scientific Instruments, 75, 1988 (2004).


5. C. P. Green and J. E. Sader, Journal of Applied Physics, 92, 262 (2002).


6. J. E. Sader et al., Journal of Applied Physics, 97, 124903 (2005).


7. J. E. Sader, Review of Scientific Instruments, 83, 103705 (2012).


8. J. E. Sader et al., Review of Scientific Instruments, 87, 093711 (2016).